♥数据结构基础知识体系详解♥
♥数据结构基础知识体系详解♥
提示
对于数据结构这种基础内容,在构建其知识体系时要避免自己再造轮子,需要高一点层次整体上去理解它(格局要大一点,不要盯着代码),要了解算法思想,性能及适用场景,用一些工具和别人梳理的结果帮助自己构建知识体系等。
知识体系
知识体系系统性梳理
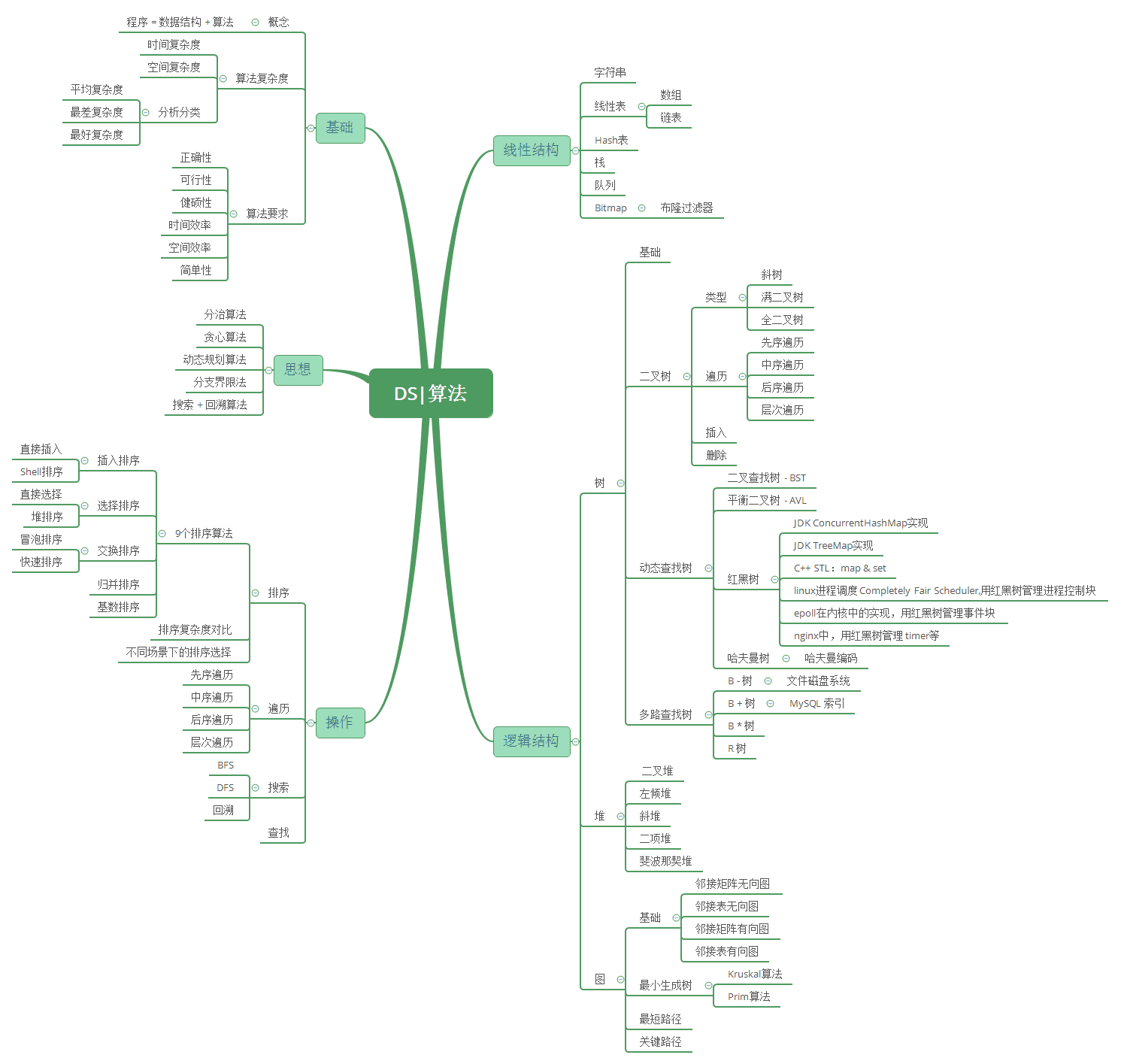
学习思路
避免孤立的学习知识点,要关联学习。比如实际应用当中,我们经常使用的是
查找和排序操作,这在我们的各种管理系统、数据库系统、操作系统等当中,十分常用,我们通过这个线索将知识点串联起来:
数组的下标寻址十分迅速,但计算机的内存是有限的,故数组的长度也是有限的,实际应用当中的数据往往十分庞大;而且无序数组的查找最坏情况需要遍历整个数组;后来人们提出了二分查找,二分查找要求数组的构造一定有序,二分法查找解决了普通数组查找复杂度过高的问题。任何一种数组无法解决的问题就是插入、删除操作比较复杂,因此,在一个增删查改比较频繁的数据结构中,数组不会被优先考虑
普通链表由于它的结构特点被证明根本不适合进行查找
哈希表是数组和链表的折中,同时它的设计依赖散列函数的设计,数组不能无限长、链表也不适合查找,所以也不适合大规模的查找
二叉查找树因为可能退化成链表,同样不适合进行查找
AVL树是为了解决可能退化成链表问题,但是AVL树的旋转过程非常麻烦,因此插入和删除很慢,也就是构建AVL树比较麻烦
红黑树是平衡二叉树和AVL树的折中,因此是比较合适的。集合类中的Map、关联数组具有较高的查询效率,它们的底层实现就是红黑树。
多路查找树 是大规模数据存储中,实现索引查询这样一个实际背景下,树节点存储的元素数量是有限的(如果元素数量非常多的话,查找就退化成节点内部的线性查找了),这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下。
B树与自平衡二叉查找树不同,B树适用于读写相对大的数据块的存储系统,例如磁盘。它的应用是文件系统及部分非关系型数据库索引。
B+树在B树基础上,为叶子结点增加链表指针(B树+叶子有序链表),所有关键字都在叶子结点 中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中。通常用于关系型数据库(如Mysql)和操作系统的文件系统中。
B*树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针, 在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3。
R树是用来做空间数据存储的树状数据结构。例如给地理位置,矩形和多边形这类多维数据建立索引。
Trie树是自然语言处理中最常用的数据结构,很多字符串处理任务都会用到。Trie树本身是一种有限状态自动机,还有很多变体。什么模式匹配、正则表达式,都与这有关。
相关文章
A. 数据结构 知识点:数据结构是基础中的基础,任何进阶都逃不开这些知识点。
B. 数据结构之 线性结构:首先理解数据结构中线性结构及其延伸:数组和矩阵,链表,栈和队列等。
- 线性表 - 数组和矩阵
- 数组是一种连续存储线性结构,元素类型相同,大小相等,数组是多维的,通过使用整型索引值来访问他们的元素,数组尺寸不能改变
- 线性表 - 链表
- n个节点离散分配,彼此通过指针相连,每个节点只有一个前驱节点,每个节点只有一个后续节点,首节点没有前驱节点,尾节点没有后续节点。确定一个链表我们只需要头指针,通过头指针就可以把整个链表都能推出来
- 线性表(散列) - 哈希表
- 散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
- 线性表 - 栈和队列
- 数组和链表都是线性存储结构的基础,栈和队列都是线性存储结构的应用
C. 数据结构之 逻辑结构:树:然后理解数据结构中逻辑结构之树:二叉搜索树(BST),平衡二叉树(AVL),红黑树(R-B Tree),哈夫曼树,前缀树(Trie)等。
- 树 - 基础和Overview
- 树在数据结构中至关重要,这里展示树的整体知识体系结构和几种常见树类型
- 树 - 二叉搜索树(BST)
- 本文主要介绍 二叉树中最基本的二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
- 树 - 平衡二叉树(AVL)
- 平衡二叉树(Balanced Binary Tree)具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列,可以参考Fibonacci数列,1是根节点,F(n-1)是左子树的节点数量,F(n-2)是右子树的节点数量。
- 树 - 红黑树(R-B Tree)
- 红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组,是平衡二叉树和AVL树的折中。
- 树 - 哈夫曼树
- 哈夫曼又称最优二叉树, 是一种带权路径长度最短的二叉树。
- 树 - 前缀树(Trie)
- Trie,又称字典树、单词查找树或键树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
D. 数据结构之 逻辑结构:图:最后理解数据结构中逻辑结构之图:图基础,图的遍历,最小生成树(Prim & Kruskal),最短路径(Dijkstra & Frolyd),拓扑排序(Topological sort),AOE & 关键路径等。
- 图 - 基础和Overview
- 图(Graph)是由顶点和连接顶点的边构成的离散结构。在计算机科学中,图是最灵活的数据结构之一,很多问题都可以使用图模型进行建模求解。例如: 生态环境中不同物种的相互竞争、人与人之间的社交与关系网络、化学上用图区分结构不同但分子式相同的同分异构体、分析计算机网络的拓扑结构确定两台计算机是否可以通信、找到两个城市之间的最短路径等等。
- 图 - 遍历(BFS & DFS)
- 图的深度优先搜索(Depth First Search),和树的先序遍历比较类似; 广度优先搜索算法(Breadth First Search),又称为"宽度优先搜索"或"横向优先搜索"
- 图 - 最小生成树(Prim & Kruskal)
- Kruskal算法是从最小权重边着手,将森林里的树逐渐合并;prim算法是从顶点出发,在根结点的基础上建起一棵树
- 图 - 最短路径(Dijkstra & Frolyd)
- 最短路径有着广泛的应用,比如地图两点间距离计算,公交查询系统,路由选择等
- 图 - 拓扑排序(Topological sort)
- 拓扑排序主要用来解决有向图中的依赖解析(dependency resolution)问题
- 图 - AOE & 关键路径
- 关键路径在项目管理计算工期等方面有广泛等应用,提升工期就是所见缩减所有关键路径上的工期,并且在实现时需要应用到之前拓扑排序的算法(前提: 有向无环图,有依赖关系)
入门推荐
- 强烈推荐用动画学习算法 Data Structure Visualizations在新窗口打开
- 推荐一个学习数据结构的英文网站 Java Point - DS在新窗口打开
- 推荐Github上java算法集合 TheAlgorithms - Java在新窗口打开
- 推荐@skywang12345写的数据结构 skywang12345 - DS在新窗口打开
- 推荐@QG-whz数据结构图画的好(本章节中有部分图源于这位作者) QG-whz在新窗口打开
- 推荐@亦海数据结构的文章,写的很清晰 亦海 - DS在新窗口打开
进阶推荐
- 首推@July结构之法 算法之道 July - 结构之法 算法之道在新窗口打开