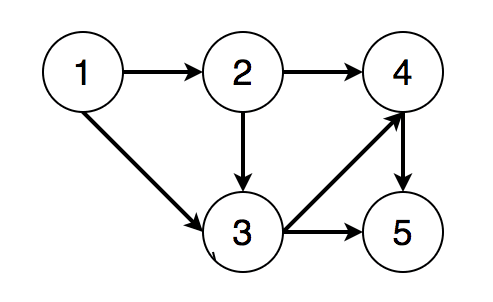
图 - AOE & 关键路径
关键路径在项目管理计算工期等方面有广泛等应用,提升工期就是所见缩减所有关键路径上的工期,并且在实现时需要应用到之前拓扑排序的算法(前提: 有向无环图,有依赖关系)。
关键路径相关名词
相关术语:
AOV网络(Activity On Vertex Network): 有向图,用顶点表示活动,用弧表示活动的先后顺序AOE网络(Activity On Edge): 有向图,用顶点表示事件,用弧表示活动,用权值表示活动消耗时间(带权的有向无环图)活动: 业务逻辑中的行为,用边表示事件: 活动的结果或者触发条件关键路径: 具有最大路径长度(权重)的路径,可能不止一条活动的两个属性: e(i)最早开始时间,l(i)最晚开始时间事件的两个属性: ve(j)最早开始时间,vl(j)最晚开始时间